La Parábola

Se llama parábola al lugar geométrico de los puntos del plano que equidistan de un punto fijo, llamado foco, y de una recta fija llamada directriz.

Elementos de la parábola

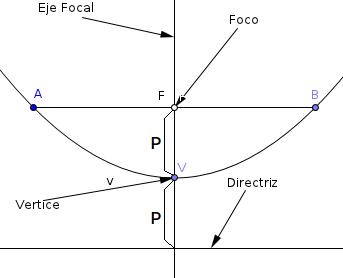
Directriz

La directriz es la recta sobre la cual, si medimos su distancia hasta un punto cualquiera de la parábola, esta debe ser igual a la distancia de ese mismo punto al foco.

Eje Focal

El eje focal es la recta perpendicular a la directriz que pasa por el foco.

Vértice

Es el punto en el cual la parábola corta el eje focal.

Lado Recto

Es un segmento paralelo a la directriz, que pasa por el foco y es perpendicular al eje focal y sus extremos son puntos de la parábola (A,B).

Parámetro

La distancia entre el vértice y la directriz que es la misma entre el vértice y el foco recibe el nombre de parámetro de la parábola (suele denotarse por p).

El eje focal funciona también como eje de simetría: al reflejar cualquier punto respecto a él se obtiene otro punto de la misma curva. Esta propiedad agiliza el trazado de la gráfica porque basta calcular algunos puntos con valores positivos de x y replicarlos al otro lado del eje.

Tipos de parábolas

Una parábola puede abrirse hacia arriba, abajo, derecha o izquierda. Si su eje es paralelo al eje y, la ecuación básica es (x - h)² = 4p(y - k) y el signo de p indica si se abre hacia arriba (p > 0) o hacia abajo (p < 0). Cuando el eje es paralelo al eje x se usa (y - k)² = 4p(x - h) y el signo de p determina si se abre a la derecha o a la izquierda. Identificar la orientación facilita interpretar tablas de valores y gráficas en el cuaderno.

Lectura de la ecuación

Si conoces la ecuación y = 2x², puedes hallar el parámetro porque 4p = 1/2 y, por tanto, p = 1/8. Eso significa que el foco está a 0.125 unidades sobre el vértice y que el lado recto mide 0.25 unidades. Trabajar con valores sencillos (por ejemplo y = (1/4)x² o x = -3y²) refuerza la relación entre la expresión algebraica y el dibujo.

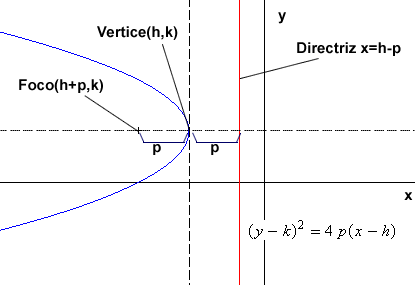
Ecuación de la parábola

La ecuación para una parábola con eje focal paralelo al eje x, vértice en (h,k) y cuya distancia al foco es p es:

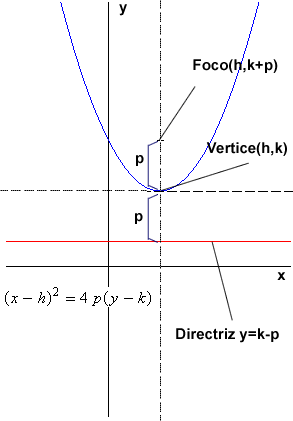
La ecuación para una parábola con eje focal paralelo al eje y, vértice en (h,k) y cuya distancia al foco es p es:

Construcción

Se debe tomar una hoja de acetato; en ella se dibuja un punto. Para construir la parábola se dobla la hoja de tal manera que cualquier punto del borde inferior coincida con el punto dibujado y desdoblamos la hoja. Repitiendo el procedimiento con distintos puntos del borde inferior, las marcas de los dobleces forman una parábola. El punto dibujado es el foco y el borde inferior de la hoja, la directriz.

Otra forma de encontrar una parábola es realizar un corte a un cono de unicel con un plano cuya dirección vaya desde la base del cono a cualquier punto del mismo. El perímetro del corte será una parábola.

Aplicaciones

Las aplicaciones de las parábolas se enfocan en hacer converger o diverger haces de luz y sonido. Ejemplos comunes incluyen antenas parabólicas, lámparas sordas, faros de automóviles, hornos solares y micrófonos paraboloidales.

Si se coloca una bombilla encendida en el foco de la parábola, los haces reflejados se vuelven perpendiculares a la directriz. Este principio explica el funcionamiento de faros y paraboloides reflectores. También sustenta el diseño de las antenas parabólicas y de ciertos telescopios.

En el siglo XVI Galileo demostró que la trayectoria de un proyectil disparado formando un ángulo con la horizontal es una parábola. Desde entonces, las formas parabólicas se emplean en fanales de automóviles, telescopios reflectores y puentes colgantes.

Ecuación simple

Obtenemos una ecuación simplificada para una parábola si colocamos su vértice en el origen y su directriz paralela al eje x. Si el foco es el punto (0,p) entonces la directriz tiene la ecuación y = -p y la parábola tiene la ecuación x² = 4py.

Si escribimos a = 1/(4p), la ecuación toma la forma y = ax². La parábola se abre hacia arriba si a > 0 y hacia abajo si a < 0. La gráfica es simétrica respecto al eje Y porque su ecuación no cambia cuando x se reemplaza por -x.

Si intercambiamos x e y en la ecuación anterior, el resultado es una parábola cuya directriz es paralela al eje Y con la ecuación x = ay², que se abre hacia la derecha si a > 0 y hacia la izquierda si a < 0.

Ecuación general

Para una parábola con eje focal paralelo al eje x: (y - k)² = 4p(x - h). Al desarrollar se obtiene y² - 2ky - 4px + k² + 4ph = 0. Tomando -2k como D, -4p como E y k² + 4ph como F resulta y² + Dy + Ex + F = 0.

Para una parábola con eje focal paralelo al eje y: (x - h)² = 4p(y - k). Al desarrollar se obtiene x² - 2hx - 4py + h² + 4pk = 0 y, con -2h como D, -4p como E y h² + 4pk como F, resulta x² + Dx + Ey + F = 0.

Actividades recomendadas

1) Traza la directriz y el foco en tu cuaderno cuadriculado, elige varios puntos del borde inferior y verifica con una regla que la distancia al foco y a la directriz sea la misma. 2) Usa una cuerda corta (del largo del lado recto) para marcar la forma en una cartulina. 3) Modela un reflector improvisado con papel aluminio y comprueba cómo concentra la luz en el foco. Estas propuestas enlazan la teoría con experimentos sencillos y seguros.

También puedes emplear una aplicación de graficación: introduce diferentes ecuaciones de parábolas e identifica cómo cambian el vértice, el foco y la amplitud al modificar los coeficientes. Registrar las observaciones en una tabla comparativa ayuda a crear un resumen visual para futuros repasos.

Métodos para obtener la ecuación

Si cuentas con el vértice y otro punto de la parábola, la forma (x - h)² = 4p(y - k) permite despejar p sustituyendo las coordenadas del punto conocido. Cuando conoces el foco y la directriz, aplica la definición de distancia: iguala la distancia desde (x,y) al foco con la distancia desde (x,y) a la directriz y reduce la expresión hasta obtener la ecuación general. Practicar ambos procedimientos refuerza la comprensión del concepto de lugar geométrico.

También puedes partir de una tabla de datos experimentales (por ejemplo, la altura de un chorrito de agua cada cierto tiempo) y ajustar una función cuadrática con calculadora u hoja de cálculo. Anotar el proceso enseña cómo las parábolas modelan movimientos reales y cómo se conectan el trabajo manual y el digital.

Errores frecuentes

• Confundir el valor de p con la distancia entre focos (la parábola solo tiene un foco).
• Olvidar que el lado recto mide 4p cuando la ecuación está en forma canónica.
• No trazar el eje de simetría, lo que provoca gráficas asimétricas.
• Intercambiar las coordenadas del foco al moverse de una parábola vertical a una horizontal.
• Descuidar las unidades al trabajar con aplicaciones de física, lo que altera la altura o el alcance.

Guía para resolver ejercicios

1) Identifica qué datos te entregan: foco y directriz, vértice y punto, o una ecuación ya dada. 2) Dibuja un esquema rápido con el eje de simetría y anota allí las distancias conocidas. 3) Usa la forma adecuada ((x - h)² = 4p(y - k) o (y - k)² = 4p(x - h)) y sustituye para hallar p. 4) Comprueba tu respuesta calculando la distancia al foco y a la directriz para un punto cualquiera.

Prueba rápida de repaso

- Explica con tus palabras por qué todos los puntos de la parábola equidistan del foco y la directriz.
- Menciona dos objetos reales que utilicen una parábola y describe qué elemento corresponde al foco.
- Resuelve en tu cuaderno: encuentra la ecuación de la parábola con vértice en (0,0) y foco en (0,3).
- Calcula el lado recto si p = 2 y dibuja la gráfica a escala.